Pada dasarnya tabel regresi SPSS adalah sebagai berikut:

Gambar (1) : Tabel untuk mengetahui tingkat pengaruh variabel

Gambar (2) : Tabel untuk mengetahui keberpengaruhan variabel dan koefisien regresi

Tabel dalam SPSS untuk regresi memang ada beberapa, namun hanya dua tabel tersebut yang perlu mendapat perhatian. Perhatikan pada gambar kedua terlebih dahulu. Pada kolom terakhir yaitu pada nilis sig terdapat nilai sig .000, artinya nilai tersebut signifikan karena kurang dari 0,05.

Karena signifikan artinya ada pengaruh antara variabel kemahiran proses dan variabel penguasaan kompetensi (pada analisis ini saya menggunakan variabel kemahiran proses sebagai independet variabel untuk penguasaan kompetensi sebagai dependent variabelnya). Kita tidak perlu memahami makna angka lain pada kolom yang sama.

Beralih ke gambar (1), setelah diketahui bahwa kedua variabel saling berpengaruh, maka tahapan berikutnya kita akan mencari tahu seberapa besar kontribusi yang diberikan variabel kemahiran kepada penguasaan kompetensi. Perhatikan pada kolom R square di atas! Disana terdapat angka ,222 artinya bahwa kemahiran memberikan kontribusi sebesar 0,222 atau 22,2% terhadap hasil penguasaan kompetensi. Artinya 77,8% hasil penguasaan dipengaruhi oleh faktor lain yang tidak terangkum dalam analisis ini.

Catatan Pakdhe : Mengenai besar kecil pengaruh suatu variabel akan saya tulis dilain waktu.

Kembali ke gambar (2), langkah berikutnya adalah mengetahui rumus persamaan regresinya. Secara umum persamaan regresi adalah:

Y = a + bX

dengan Y adalah variabel dependent, dalam hal ini adalah penguasaan kompetensi, dan X adalah variabel independent, dalam hal ini adalah kemahiran berproses. Sedangkan a dan b adalah nilai konstanta yang dicari.

Catatan Pakdhe : Ulasan lengkap mengfenai variabel ada disini.

Berdasarkan gambar (2) diketahui nilai constant-nya adalah -11,409 dan nilai kemahiran berprosesnya adalah 4,505. Dari keterangan tersebut kita dapat memperoleh persamaan regresi sebagai berikut:

Y = -11,409 + 4,505X

Artinya, ketika siswa kita memperoleh skor kemahiran sebesar 22 maka dapat diprediksi bahwa skor tes penguasaan kompetensi siswa tersebut adalah :

Y = -11,409 + 4,505 . 22 = -11,409 + 99,11 = 87,701

Selamat Belajar

Cara menganalisis Regresi linier berganda dengan SPSS 17.0

Analisis regresi digunakan untuk memprediksi pengaruh variabel bebas terhadap variabel terikat. Analisis regresi juga dapat dilakukan untuk mengetahui kelinieritas variabel terikat dengan varibel bebasnya, selain itu juga dapat menunjukkan ada atau tidaknya data yang outlier atau data yang ekstrim.
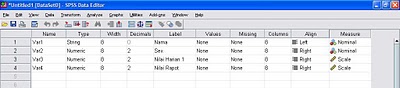
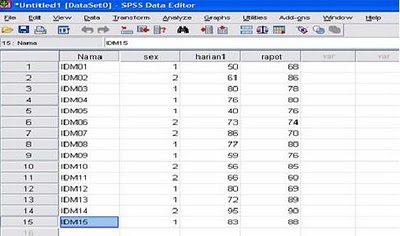
Analisis regresi linear berganda terdiri dari satu variabel dependen dan dua atau lebih variabel independen. Misalnya dalam suatu kegiatan penelitian ingin diketahui apakah variabel X (Sex dan Nilai harian 1) berpengaruh terhadap variabel Y (nilai rapot). Data penelitian adalah sebagai berikut:

Nama	Sex	Nilai harian 1	Nilai Rapot
IDM01 IDM02 IDM03 IDM04 IDM05 IDM06 IDM07 IDM08 IDM09 IDM10 IDM11 IDM12 IDM13 IDM14 IDM15	1 2 1 1 1 2 2 1 1 2 2 1 1 2 1	50 61 80 76 40 73 86 77 59 56 66 80 72 95 83	68 86 78 80 76 74 70 80 76 85 60 69 89 90 88

Keterangan sex: 1=laki-laki, 2=perempuan

Langkah-langkah menganalisis menggunakan spss 17.0 adalah sebagai berikut:
1. Buka lembar kerja SPSS
2. Buat semua keterangan variabel di variable view seperti gambar berikut:

3. Klik Data view dan masukan data sehingga tampak hasilnya sebagai berikut:

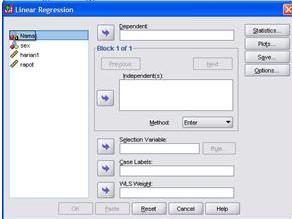
4. Lakukan analisis dengan cara: Analize, Regression, Liniear. akan muncul dialog seperti gambar berikut; Selanjutnya isilah kotak menu Dependen dengan variabel terikat, yaitu variabel Rapor dan kotak menu independen dengan variabel bebas, yaitu variabel Sex dan Harian 1.

5. Selanjutnya klik kotak menu Statistics. Pilih Estimates, Descriptives dan Model fit lau klik Continue. Tampilan muncul seperti berikut

6. Kotak menu Plots, berfungsi untuk menampilkan grafik pada analisis regresi. klik kotak menu Plots, kemudian klik Normal probanility plot yang terletak pada kotak menu Standardized Residual plots. Selanjutnya klik Continue. Tampilannya adalah sebagai berikut:

7. Selanjutnya klik Continue. Untuk melakukan analisis kliklah OK. Beberapa saat kemudian akan keluar outputnya, sebagai berikut:

Regression

[DataSet1]

Cara membaca Output tersebut adalah. sebagai berikut:
1. Deskriptif statistik

Dari output tersebut dapat dilihat rata-rata nilai rapot dari 15 siswa adalah 77,93 dengan standar deviasi 8,779 sedangkan rata-rata nilai harian 1 adalah 70,27 dengan standar deviasi 14,786

2. Korelasi

Dari tabel dapat dilihat bahwa besar hubungan antara variabel nilai rapot dengan sex adalah -0,042 hal ini menunjukan hubungan negatif.
besar hubungan nilai harian 1 dengan nilai rapot adalah 0,238 yang berarti ada hubungan positif, makin besar nilai harian 1 maka makin tinggi pula nilai rapot.

3. Variabel masuk dan keluar

Dari tabel diatas menunjukan variabel yang dimasukan adalah nilai harian 1 dan sex, sedangkan variabel yang dikeluarkan tidak ada (Variables Removed tidak ada)

4.Model sisaan

Pada tabel diatas angka R Square adalah 0,063 yaitu hasil kuadrat dari koefisien korelasi (0,250 x 0,250 = 0,063). Standar Error of the Estimate adalah 9,181, perhatikan pada analisis deskriptif statitik bahwa standar deviasi nilai rapot adalah 8,779 yang jauh lebih kecil dari dari standar error, oleh karena lebih besar daripada standar deviasi nilai rapot maka model regresi tidak bagus dalam bertindak sebagai predictor nilai rapot.

5. Anova

Hipotesis:
Ho: B1=B2=0
Ha: ada Bi yang tidak nol
Pengambilan keputusan:
Jika F hitung <= T tabel atau probabilitas >= 0,05 maka Ho diterima
Jika F hitung > T tabel atau probabilitas < 0,05 maka Ho ditolak

Dari tabel diatas dapat dilihat nilai F hitung yaitu 0,401, sedangkan nilai F tabel dapat diperoleh dengan menggunakan tabel F dengan derajat bebas (df) Residual (sisa) yaitu 12 sebagai df penyebut dan df Regression (perlakuan) yaitu 2 sebagai df pembilang dengan tarap siginifikan 0,05, sehingga diperoleh nilai F tabel yaitu 3,89. Karena F hitung (0,401) < F tebel (3,89) maka Ho diterima.
Berdasarkan nilai Signifikan, terlihat pada kolom sig yaitu 0,679 itu berarti probabilitas 0,679 lebih dari daripada 0,05 maka Ho diterima.
Kesimpulan:
Tidak ada koefisien yang tidak nol atau koefisien berarti, maka model regresi tidak dapat dipakai untuk memprediksi nilai rapot.

6. Koefisien

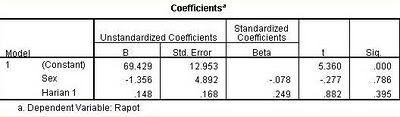
Hipotesis:
Ho: Bi=0
Ha: ada Bi yang tidak nol , i=1 atau 2
Pengambilan keputusan:
Jika T hitung <= T tabel atau probabilitas >= 0,05 maka Ho diterima
Jika T hitung > T tabel atau probabilitas < 0,05 maka Ho ditolak
* Constant: Berdasarkan tabel diatas, dapat dilihat bahwa nilai T hitung untuk Constant yaitu 5,360, pada T tabel dengan db 12 dan taraf signifikan 0,05 diperoleh 1,782, karena T hitung > T tabel maka Ho ditolak. sedangkan sig pada tabel B adalah 0,000 yang berarti probabilitas 0,000, karena probabilitas kurang dari 0,05 maka ditolak. Berarti bermakna dan diramalkan tidak melalui titik (0,0).
** Sex: Berdasarkan tabel diatas, dapat dilihat bahwa nilai T hitung untuk Sex yaitu -0,277, pada T tabel dengan db 12 dan taraf signifikan 0,05 diperoleh 1,782, karena T hitung < T tabel maka Ho diterima. sedangkan sig pada tabel B adalah 0,786 yang berarti probabilitas 0,786, karena probabilitas kurang dari 0,05 maka diterima. artinya B tidak berarti.
*** Harian 1: Berdasarkan tabel diatas, dapat dilihat bahwa nilai T hitung untuk Harian 1 yaitu 0,882, pada T tabel dengan db 12 dan taraf signifikan 0,05 diperoleh 1,782, karena T hitung < T tabel maka Ho diterima. sedangkan sig pada tabel B adalah 0,786 yang berarti probabilitas 0,395, karena probabilitas kurang dari 0,05 maka diterima. artinya B tidak berarti

Berdasarkan analisis diatas maka dapat dibuat model regresi dugaannya yaitu:
Y = 69,429

Dari tabel diatas merupakan ringkasan yang meliputi nilai minimum dan maksimum, mean dan standar deviasi dari predicted value (nilai yang diprediksi) dan statistic residu.

7. Kelinieran

Jika residual berasal dari distribusi normal, maka nilai-nilai sebaran data akan terletak sekitar garis lurus, terlihat bahwa sebaran data pada gambar diatas tersebar hampir semua tidak pada sumbu normal, maka dapat dikatakan bahwa pernyataan normalitas tidak dapat dipenuhi.

Demikian dari saya, semoga bermanfaat.

ANALISIS REGRESI DAN KORELASI SEDERHANA

Pengertian : Analisis regresi merupakan salah satu analisis yang bertujuan untuk mengetahui pengaruh suatu variabel terhadap variabel lain. Dalam analisis regresi, variabel yang mempengaruhi disebut Independent Variable (variabel bebas) dan variabel yang dipengaruhi disebut Dependent Variable (variabel terikat). Jika dalam persamaan regresi hanya terdapat satu variabel bebas dan satu variabel terikat, maka disebut sebagai persamaan regresi sederhana, sedangkan jika variabel bebasnya lebih dari satu, maka disebut sebagai persamaan regresi berganda.

Analisis Korelasi merupakan suatu analisis untuk mengetahui tingkat keeratan hubungan antara dua variabel. Tingkat hubungan tersebut dapat dibagi menjadi tiga kriteria, yaitu mempunyai hubungan positif, mempunyai hubungan negatif dan tidak mempunyai hubungan.
Analisis Regresi Sederhana : digunakan untuk mengetahui pengaruh dari variabel bebas terhadap variabel terikat atau dengan kata lain untuk mengetahui seberapa jauh perubahan variabel bebas dalam mempengaruhi variabel terikat. Dalam analisis regresi sederhana, pengaruh satu variabel bebas terhadap variabel terikat dapat dibuat persamaan sebagai berikut : Y = a + b X. Keterangan : Y : Variabel terikat (Dependent Variable); X : Variabel bebas (Independent Variable); a : Konstanta; dan b : Koefisien Regresi. Untuk mencari persamaan garis regresi dapat digunakan berbagai pendekatan (rumus), sehingga nilai konstanta (a) dan nilai koefisien regresi (b) dapat dicari dengan metode sebagai berikut :
a = [(ΣY . ΣX2) – (ΣX . ΣXY)] / [(N . ΣX2) – (ΣX)2] atau a = (ΣY/N) – b (ΣX/N)
b = [N(ΣXY) – (ΣX . ΣY)] / [(N . ΣX2) – (ΣX)2]

Contoh :
Berdasarkan hasil pengambilan sampel secara acak tentang pengaruh lamanya belajar (X) terhadap nilai ujian (Y) adalah sebagai berikut :

(nilai ujian)	X (lama belajar)	X ²	XY
40	4	16	160
60	6	36	360
50	7	49	350
70	10	100	700
90	13	169	1.170
ΣY = 310	ΣX = 40	ΣX² = 370	ΣXY = 2.740

Dengan menggunakan rumus di atas, nilai a dan b akan diperoleh sebagai berikut :
a = [(ΣY . ΣX2) – (ΣX . ΣXY)] / [(N . ΣX2) – (ΣX)2]
a = [(310 . 370) – (40 . 2.740)] / [(5 . 370) – 402] = 20,4

b = [N(ΣXY) – (ΣX . ΣY)] / [(N . ΣX2) – (ΣX)2]
b = [(5 . 2.740) – (40 . 310] / [(5 . 370) – 402] = 5,4

Sehingga persamaan regresi sederhana adalah Y = 20,4 + 5,2 X
Berdasarkan hasil penghitungan dan persamaan regresi sederhana tersebut di atas, maka dapat diketahui bahwa : 1) Lamanya belajar mempunyai pengaruh positif (koefisien regresi (b) = 5,2) terhadap nilai ujian, artinya jika semakin lama dalam belajar maka akan semakin baik atau tinggi nilai ujiannya; 2) Nilai konstanta adalah sebesar 20,4, artinya jika tidak belajar atau lama belajar sama dengan nol, maka nilai ujian adalah sebesar 20,4 dengan asumsi variabel-variabel lain yang dapat mempengaruhi dianggap tetap.
Analisis Korelasi (r) : digunakan untuk mengukur tinggi redahnya derajat hubungan antar variabel yang diteliti. Tinggi rendahnya derajat keeratan tersebut dapat dilihat dari koefisien korelasinya. Koefisien korelasi yang mendekati angka + 1 berarti terjadi hubungan positif yang erat, bila mendekati angka – 1 berarti terjadi hubungan negatif yang erat. Sedangkan koefisien korelasi mendekati angka 0 (nol) berarti hubungan kedua variabel adalah lemah atau tidak erat. Dengan demikian nilai koefisien korelasi adalah – 1 ≤ r ≤ + 1. Untuk koefisien korelasi sama dengan – 1 atau + 1 berarti hubungan kedua variabel adalah sangat erat atau sangat sempurna dan hal ini sangat jarang terjadi dalam data riil. Untuk mencari nilai koefisen korelasi (r) dapat digunakan rumus sebagai berikut : r = [(N . ΣXY) – (ΣX . ΣY)] / √{[(N . ΣX2) – (ΣX)2] . [(N . ΣY2) – (ΣY)2]}

Contoh :
Sampel yang diambil secara acak dari 5 mahasiswa, didapat data nilai Statistik dan Matematika sebagai berikut :

Sampel	X (statistik)	Y (matematika)	XY	X²	Y²
1	2	3	6	4	9
2	5	4	20	25	16
3	3	4	12	9	16
4	7	8	56	49	64
5	8	9	72	64	81
Jumlah	25	28	166	151	186

r = [(N . ΣXY) – (ΣX . ΣY)] / √{[(N . ΣX2) – (ΣX)2] . [(N . ΣY2) – (ΣY)2]}
r = [(5 . 166) – (25 . 28) / √{[(5 . 151) – (25)2] . [(5 . 186) – (28)2]} = 0,94

Nilai koefisien korelasi sebesar 0,94 atau 94 % menggambarkan bahwa antara nilai statistik dan matematika mempunyai hubungan positif dan hubungannya erat, yaitu jika mahasiswa mempunyai nilai statistiknya baik maka nilai matematikanya juga akan baik dan sebaliknya jika nilai statistik jelek maka nilai matematikanya juga jelek.

CONTOH KASUS ANALISISREGRESI DAN KORELASI SEDERHANA

Seorang peneliti ingin mengetahui pengaruh dari tinggi badan terhadap berat badan. Untuk kebutuhan penelitian tersebut diambil sampel secara acak sebanyak 10 orang untuk diteliti. Hasil pengumpulan data diketahui data sebagai berikut :

Berdasarkan data tersebut di atas :

Hitunglah nilai a dan b untuk persamaan regersi linier sederhana
Jika hipotesis penelitian menyatakan bahwa “tinggi badan seseorang berpengaruh terhadap berat badan seseorang”, ujilah hipotesis tersebut dengan menggunakan Uji T dan Uji F (tingkat keyakinan sebesar 95%)
Hitunglah nilai r dan koefisien determinasi
Bagaimana kesimpulannya.

Jawab :

Hipotesis penelitian : Tinggi Badan berpengaruh terhadap Berat Badan Seseorang (karena hanya dikatakan berpengaruh maka menggunakan uji dua arah).
Jika Y : Berat Badan Seseorang dan X : Tinggi Badan Seseorang, maka untuk mendapatkan nilai a dan b untuk persamaan regersi linier sederhana :

Berdasarkan hasil pengolahan data tersebut di atas maka dapat dibuat persamaan regresi linier sederhana : Y = - 73,72041 + 0,819657 X

Untuk menguji hipotesis secara parsial digunakan Uji T, yaitu :

Hipotesis Statistik adalah Ho : b = 0 dan Ha : b ≠ 0 (disebut uji dua arah)

Nilai T hitung adalah : b/Sb = 0,819657/0,05525673 = 14,833613932638 = 14,834

Nilai T tabel dengan df : 10 – 2 = 8 dan ½ α = 2,5% (uji dua arah) sebesar ± 2,306

Karena nilai T hitung lebih besar dari pada T tabel atau 14,834 > 2,306 maka Ho ditolak, Ha diterima dan hipotesis penelitian yang menyatakan bahwa Tinggi Badan berpengaruh terhadap Berat Badan Seseorang adalah dapat diterima (dapat dikatakan signifikan secara statistik).

Sedangkan untuk menguji secara serempak digunakan Uji F, yaitu diperoleh F hitung = 31.874,98 dan Untuk nilai F tabel dengan df : k - 1 ; n – k = 1 ; 8 dan α : 5% sebesar 5,32. Karena nilai F hitung lebih besar dari F tabel atau 31.874,98 > 5,32 maka Ho ditolak, Ha diterima dan hipotesis penelitian yang menyatakan bahwa Tinggi Badan berpengaruh terhadap Berat Badan Seseorang adalah dapat diterima.

Untuk nilai r (korelasi) adalah sebesar 0,982 dan koefisien determinasi (r kuadrat) sebesar 0,964. Berdasarkan hasil nilai koefisien korelasi maka dapat dikatakan bahwa hubungan antara variabel independen (Tinggi Badan) dengan variabel dependen (Berat Badan) mempunyai hubungan yang kuat karena nilai r sebesar 98,2% tersebut sangat mendekati nilai 100%.
Sedangkan berdasarkan nilai r kuadrat sebesar 96,4% menggambarkan bahwa sumbangan variabel independen (Tinggi Badan) terhadap naik turunnya variabel dependen (Berat Badan) sebesar 96,4% sedangkan sisanya merupakan sumbangan dari variabel lain yang tidak dimasukkan dalam model.

Kesimpulannya :
Berdasarkan hasil pengujian hipotesis, baik Uji T maupun Uji F, diketahui bahwa Variabel Tinggi Badan Seserorang berpengaruh terhadap Variabel Berat Badan Seseorang dan pengaruhnya bersifat positif (nilai koefisien regresinya sebesar 0,819657), artinya jika seseorang mempunyai tinggi badan semakin tinggi maka akan meningkatkan berat badannya (dan sebaliknya). Berdasarkan nilai koefisien regresi tersebut dapat diketahui bahwa jika tinggi badan meningkat sebesar 10% maka berat badan akan meningkat 8,2%.
Sedangkan berdasarkan nilai koefisien korelasi dan koefisien determinasi diketahui bahwa variabel independen (Tinggi Badan) mempunyai hubungan yang kuat dan mempunyai sumbangan yang cukup besar terhadap variabel dependen (Berat Badan).